
*예전에 제가 운영했던 블로그의 재업로드 글임을 밝힙니다.
https://schonemath.tistory.com/2
피타고라스의 정리(Pythagorean theorem)의 여러가지 증명법(1)
오늘은 피타고라스의 정리의 여러 가지 증명법을 알아보도록 하겠습니다. (중학교 2~3학년 수준의 수학을 알고 계시다면 이해하는 데는 큰 무리가 없을 거라 생각합니다) 피타고라스의 정리는
schonemath.tistory.com
오늘은 피타고라스의 정리의 여러 가지 증명법을 알아보도록 하겠습니다.
(중학교 2~3학년 수준의 수학을 알고 계시다면 이해하는 데는 큰 무리가 없을 거라 생각합니다)
피타고라스의 정리는 여러가지 공식을 유도하는 데에도 사용됩니다.
그 예시로는 코사인 법칙 등이 있습니다.
그럼 먼저 피타고라스의 정리 공식 내용부터 알아보도록 하겠습니다.
1) 공식
피타고라스 정리의 내용은 다음과 같습니다.


빗변의 제곱은 두변의 제곱의 합과 같다.
2) 증명
피타고라스의 정리는 알려진 증명 방법만 400가지가 넘습니다. 오늘은 그중 3가지 방법에 대해 알아보도록 하겠습니다.
-1. 직각삼각형의 닮음을 이용한 증명(1)
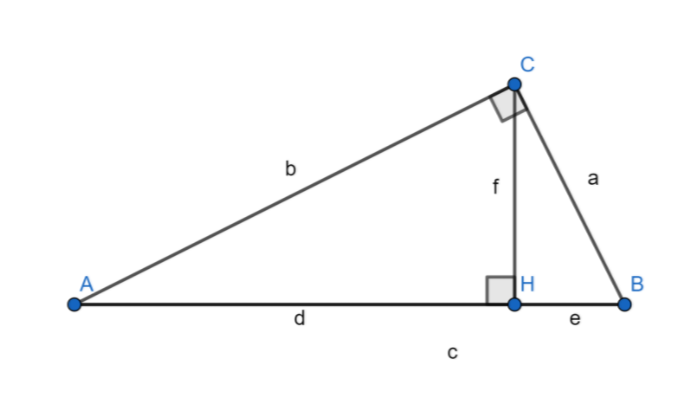
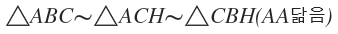
삼각형 ABC와 삼각형 ACH가 닮음이므로

내항의 곱과 외항의 곱은 같으므로

삼각형 ABC와 삼각형 CBH가 닮음이므로

내항의 곱과 외항의 곱은 같으므로

②에 ①을 더하면

d+e는 c와 같으므로
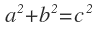
피타고라스의 정리가 성립함을 알 수 있습니다.
-2. 직각삼각형의 닮음을 이용한 증명(2)

이 그림에서 삼각형 ABC와 삼각형 ACH는 각 A가 공통이고 직각삼각형이므로 AA닮음, 삼각형 ABC와 삼각형 CBH는 각 B가 공통이고 직각삼각형이므로 AA닮음, 삼각형 ABC와 삼각형 ACH가 닮음이고, 삼각형 ABC와 삼각형 CBH가 닮음이므로, 세 직각삼각형은 닮음임을 알 수 있게 됩니다.

세 직각삼각형은 AA닮음이므로 a:b:c라는 닮음비를 가지게 됩니다.
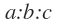
이때, 세 삼각형의 넓이의 비는
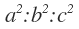
삼각형 ABC의 넓이는 다른 두 삼각형 넓이의 합과 같으므로

피타고라스의 정리가 성립함을 알 수 있습니다.
-3. 가필드의 증명

삼각형 ABC와 삼각형 DEB는 합동인 삼각형이다.
사다리꼴 ADCE의 넓이는

삼각형 ABC, 삼각형 DEB, 삼각형 CBE 넓이의 합은

사다리꼴 ADCE의 넓이는 삼각형 ABC, 삼각형 DEB, 삼각형 CBE 넓이의 합과 같으므로

정리하면

피타고라스의 정리가 성립함을 알 수 있습니다.
공부하면서 궁금한 점이 생겼다면 꼭 댓글로 질문해주시고 도움이 되셨다면 공감이랑 구독 버튼 꾹 눌러주세요.
'기타' 카테고리의 다른 글
| [수학 교과] 2015 개정 교육과정 고등학교 수학 과목 (2) | 2023.01.28 |
|---|---|
| 코사인 법칙(the law of cosines) 증명법 (0) | 2023.01.23 |


댓글