[수치해석학] 이분법(Bisection Method)

---

 

저번에는 뉴턴-랩슨법에 대해서 글을 썼었습니다.

이번에는 뉴턴-랩슨법처럼 근사해를 구하는 방법 중 하나인 이분법을 알아보겠습니다.

 

뉴턴-랩슨법에 대해 궁금하신 분들은 아래 링크로 들어가시면 뉴턴-랩슨법과 관련된 내용을 보실 수 있습니다.

https://mathisbeatiful.tistory.com/7

[수치해석학] 뉴턴-랩슨법(Newton-Raphson Method)

---

 

1) 정의

---

이분법(Bisection Method)이란, 닫힌 구간 $[a,b]$에서 연속인 함수 $f(x)$에 대하여 $f(a)f(b)<0$인 닫힌 구간 $[a,b]$에 대하여 $\frac{a+b}{2}$을 계산한 값을 $c$라고 할 때, $a$, $b$ 중에서 $f(a)f(d)<0$를 만족시키는 $d$값을 정한 후 다시 두 값의 평균을 구할 수 있는데, 이를 반복하여 근사해를 구하는 방법입니다.

---

2) 적용 예시

---

$f(x)=x^2-1$의 근 1을 이분법으로 구하는 과정을 알아보겠습니다.

 

먼저 이분법으로 근사해를 구하려면, 근이 있을 것으로 추정되는 구간을 정해야 합니다.

볼차노의 정리에 의해  $f(a)f(b)<0$을 만족시키는 구간에는 근이 최소 하나 존재합니다.

따라서 $f(0)f(3)<0$을 만족시키는 구간인 $[0, 3]$으로 구간을 정해보도록 하겠습니다.

 

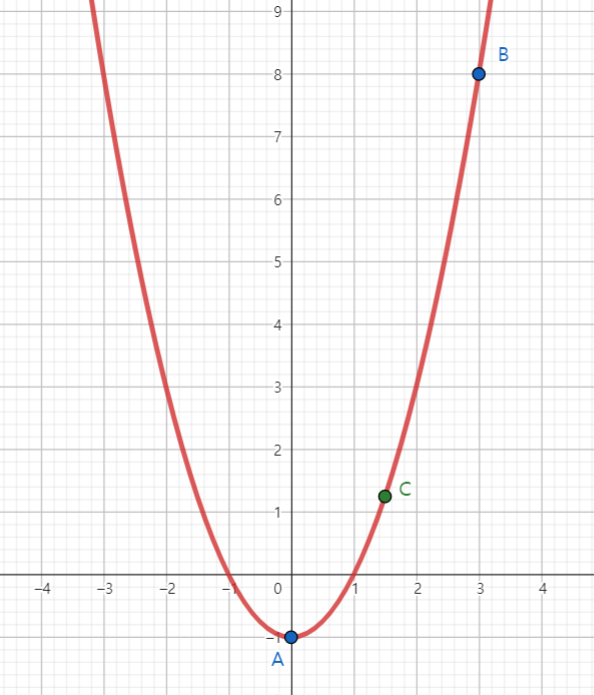
구간을 $[0, 3]$으로 정했으므로 $\frac{3+0}{2}$을 계산한 값을 $c$라고 하겠습니다.

위의 그래프처럼 $c$는 0과 3의 중간인 1.5가 되고, 구간 $[a, c]$, $[c, b]$는 구간 $[a, b]$의 절반이 됩니다.

구간 $[a, c]$, $[c, b]$ 중 $[a, c]$만이 볼차노의 정리를 만족하므로 다음 시행에서는 구간을 $[0, 1.5]$로 정하겠습니다.

 

$0.75$로 조금 더 근에 가까워진 것을 볼 수 있습니다.

다음 시행에서는 점 $C$와 점 $D$가 볼차노의 정리를 만족하므로 구간을 $[0.75, 1.5]$로 한 후 다시 중간값을 구해주시면 됩니다.

이를 반복하면 더 정확한 근사해를 구할 수 있습니다.

---

3) 장단점

---

장점

• 함수가 미분 가능하지 않아도 구할 수 있다.
• 구간 사이에 근이 존재한다면, 거의 모든 상황에서 근사해를 구할 수 있다.
• 구간의 범위가 넓은 경우 빠르게 범위를 좁힐 수 있다.

단점

• 수렴속도가 느리다. (특히, 구간이 좁을 때)
• 중근의 경우 구할 수 없다.

이 중에서 중근인 경우를 알아보겠습니다.

$y=x^2$의 경우 $x=0$에서 중근을 갖습니다.

이때, $f(a)f(d)<0$을 만족하는 구간, 즉 볼차노의 정리를 만족하는 구간이 없으므로 볼차노의 정리를 사용하는 이분법은 사용할 수 없습니다.

---

다음번에도 뉴턴-랩슨법, 이분법에 이은 근사해를 구하는 방법으로 찾아오겠습니다.

 

궁금한 점은 댓글에 남겨주세요. 제가 아는 범위 내에서 답해드리겠습니다.

이 포스팅을 읽어주셔서 감사합니다!